Schlagwörter
Zuletzt veröffentlicht
Das Königsberger Brückenproblem
Am 29. Oktober 2011 veröffentlicht von Desmond Kabus
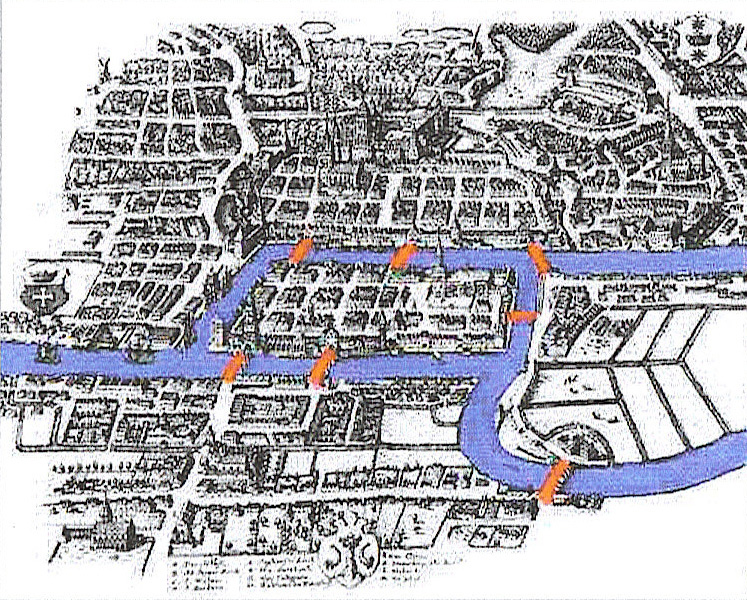
Die Abbildung zeigt die Stadt Königsberg im 18. Jahrhundert. Die beiden Arme des Flusses Pregel umfließen eine Insel, den Kneiphof. Es gibt insgesamt sieben Brücken über den Fluss.
Einige Königsberger stellten sich damals folgende Frage:
Gibt es einen Rundweg, der jede Brücke genau einmal benutzt?
Der Mathematiker Leonard Euler beantwortete 1736 diese Frage mit einer Methode, welche die moderne Graphentheorie begründete.
1.
Für die Beschreibung des Problems in der Mathematik führen wir eine symbolische Schreibweise ein. In unserer Aufgabe sind die wichtigsten Objekte die Brücken und die Gebiete. Die Folge der Brücken beschreiben zu können, führen wir zuerst Bezeichnungen für die Gebiete ein:
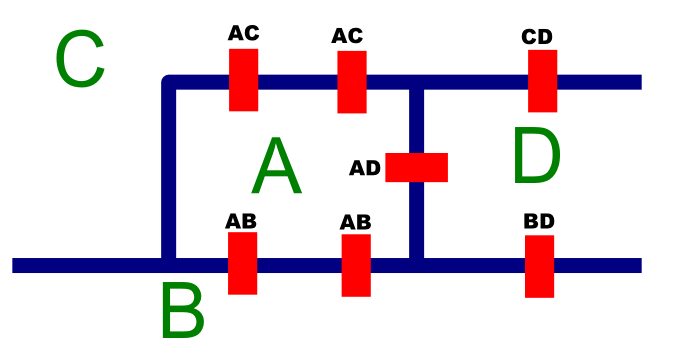
2.
Wir werden den Weg durch die Brücken, die man benutzt beschreiben. Durch Aneinanderhängen der Brückennamen in Laufrichtung (da es zwei mögliche Brückennamen gibt) ergibt sich die Wegbeschreibung.
Um die Frage, ob es einen Weg gibt, der alle Brücken genau einmal benutzt, beantworten zu können, hat sich Euler die zwei folgenden Fragen gestellt:
1. Frage |
2. Frage |
|
Wann stellt eine Kombination aus den Buchstaben A, B, C, D einen Weg dar? |
Was erfüllt der vollständige Weg zusätzlich? |
1. Antwort |
2. Antwort |
|
1. Der Weg ist eine Aneinanderreihung von Brückennamen. 2. Das Endgebiet einer Brücke ist das Startgebiet der nächsten. > Der Buchstabe dieses Gebiets kommt doppelt im Weg vor. |
1. Jede Brücke wird nur einmal benutzt. |
1. Folgerung |
2. Folgerung |
|
In dem Weg kommen alle bis auf höchstens zwei Buchstaben in gerader Anzahl vor. |
Es ist bekannt, wie oft jeder Buchstabe im Weg vorkommt. |
Schlussfolgerung:
Da sich die 1. und die 2. Folgerung widersprechen, existiert keine Lösung für einen Rundgang über die sieben Brücken in Königsberg.
Nun werden wir Eulers Vorgehensweise so verallgemeinern, dass wir für jeden beliebigen Stadtplan die Existenz eines vollständigen Rundweges überprüfen können.
Bei Königsberg gingen wir folgendermaßen vor:
Wir haben uns angeschaut, wieviele Brücken von jedem Gebiet G ausgehen. Dafür schreiben wir n(G).
Die 1. Folgerung sagt aus, dass die Anzahl n(G) für alle Gebiete (bis auf höchstens 2; bei vollständigen Rundwegen, d.h. ist das Startgebiet auch das Endgebiet, ist n(G) für alle Gebiete Gerade) gerade sein muss. Diese Bedingung bezeichnet man als Eulerbedingung.
Da die Eulerbedingung für Königsberg nicht erfüllt ist, gibt es keinen Weg.
Diese Vorgehensweise können wir auch auf andere Stadtpläne übertragen:
Wenn es den gesuchten Weg gibt, erfüllt er die Eulerbedingung
oder
Wenn die Eulerbedingung nicht erfüllt ist, gibt es auch keinen Weg
Die Eulerbedingung ist aber nur eine notwendige Bedingung: Sie allein stellt die Existenz des gesuchten Weges nicht sicher.
Die untere Anordnung soll dies veranschaulichen:
Sie werden bemerken, dass die Eulerbedingung erfüllt ist (da n(A.D) gerade), aber trotzdem existiert der Weg nicht.
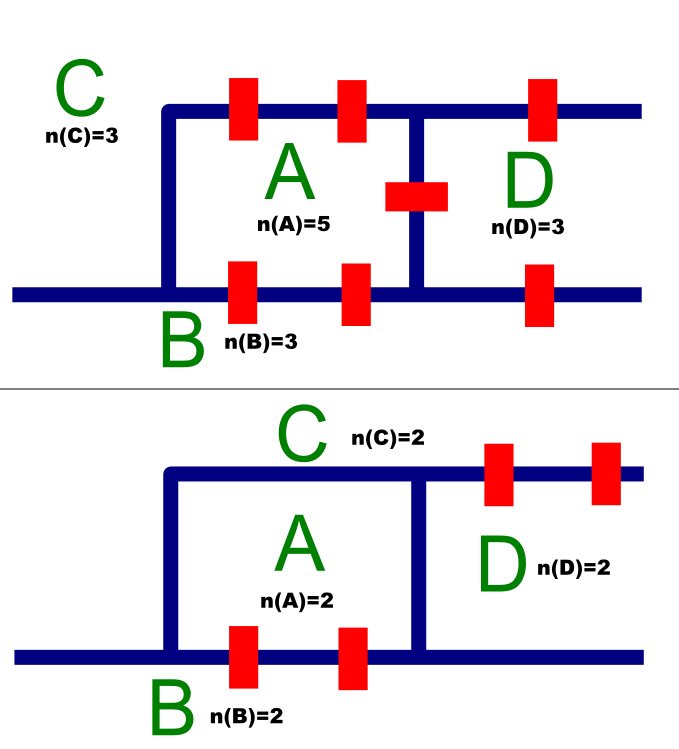
Deswegen führen wir noch eine weitere notwendige Bedingung ein:
Zusammenhangsbedingung: Von jedem Gebiet x gibt es einen Weg zu jedem anderen Gebiet y.
Die Euler- und die Zusammenhangsbedingung bilden eine hinreichende Bedingung!
Also gilt:
Bei Existenz eines vollständigen Rundweges:
n(G) ist für alle Gebiete gerade UND die Zusammenhangsbedingung ist erfüllt
Bei Existenz eines unvollständigen Rundweges:
n(G) ist für alle außer zwei Gebieten gerade UND die Zusammenhangsbedingung ist erfüllt.
